Sorting Algos
A sorting algorithm is a set of instructions that accepts an array as input, executes specified operations on the array (also known as a list), and returns a sorted array. Sorting algorithms are frequently taught early in computer science classrooms because they provide a simple way to teach other important concepts such as Big-O notation, divide-and-conquer procedures, and data structures like binary trees and heaps. When selecting a sorting algorithm, there are several things to consider.
What are they?
In other terms, a sorted array is one that is arranged in a certain order. A sorting algorithm accepts an array as input and returns a sorted permutation of that array. Integer sorting and comparison sorting are the two main types of sorting algorithms, as I will explain bellow
Comparison Sorts
At each stage of the algorithm, comparison sorts compare items to decide whether one element should be to the left or right of another.
Comparison sorts are typically easier to build than integer sorts, but comparison sorts have a lower limitation of O(n log n), which means that they can’t be quicker than O(n log n) on average (n log n). The worst-case running time of the best possible method for a particular task is known as a lower limit for an algorithm. The “on average” portion is crucial: many algorithms execute in a relatively short amount of time if the supplied list is already sorted or has some unusual (but improbable) characteristic. Because there is only one sorted permutation of a list, but n! potential lists, the chances that the input is already sorted are slim, and the list will be unsorted on average.
Integer Sorts
Counting sorts are another name for integer sorts (though there is a specific integer sort algorithm called counting sort). Because integer types do not conduct comparisons, they are not constrained by Ω(n log n). Integer sorts determine how many items are smaller than x for each element x. If there are 14 items with a value less than x, x will be assigned to the 15th position. This data is utilized to instantly insert each element in the appropriate slot, eliminating the need to reorganize lists.
Sorting Algo Properties
The aim of all sorting algorithms is to produce a sorted list, although how each algorithm does this might differ. When working with any algorithm, it’s critical to understand how quickly it runs and how much space it occupies — in other words, its time and space complexity. Comparison-based sorting algorithms have a time complexity of (nlogn), which means they can’t be quicker than n log n, as stated in the previous section. However, the running time of algorithms is generally expressed in terms of large O rather than Omega. If an algorithm has a worst-case running time of O(nlogn), it is guaranteed that it will never be slower than O(nlogn), and if it has an average-case running time of O(n2), it will never be slower than O(n2).
The running time of an algorithm indicates how many operations it must do before it completes. The space complexity of an algorithm indicates how much memory must be allocated to run it. If an algorithm takes in a list of size n and, for some reason, creates a new list of size n for each member in n, the process will use n^2 space.
It’s also useful to know if a sorting algorithm is stable when it comes to sorting algorithms.
Choosing a Algo
Consider the running time, space complexity, and desired structure of the input list while selecting a sorting algorithm for a certain issue.
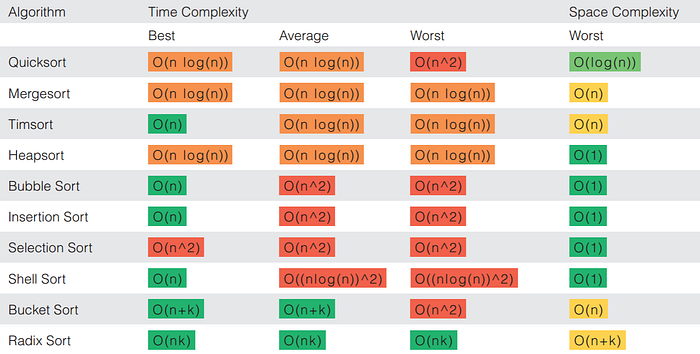
Consider these criteria while selecting a sorting algorithm. Quicksort, for example, is a fast algorithm that can be difficult to implement; bubble sort, on the other hand, is a slow algorithm that is simple to construct. Bubble sort may be a preferable alternative for sorting small quantities of data since it can be performed fast, but the speedup from quicksort may be worth the difficulty of constructing the algorithm for bigger datasets.
